Saniya Khan, Richard I. Anderson, Sylvia Ekström, Cyril Georgy, Louise Breuval

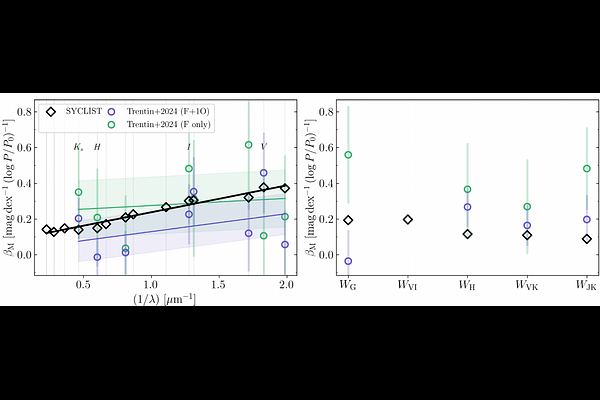
The impact of metallicity on the Cepheid Leavitt law (LL) and, in turn, the Hubble constant, has been the subject of much recent debate. Here, we present a comprehensive analysis of metallicity effects on Cepheid LLs based on synthetic Cepheid populations computed using Geneva models and the SYCLIST tool. We computed 296 co-eval populations in the age range of 5-300 Myr for metallicities representative of the Sun, the LMC, and the SMC ($Z \in [0.014, 0.006, 0.002]$). We computed LLs in fourteen optical-to-infrared passbands and five reddening-free Wesenheit magnitudes. All Cepheid populations take into account distributions of rotation rates and companion stars. We show excellent agreement between the predicted populations and key observational constraints from the literature. Our simulations predict a significant LL slope-metallicity dependence ($\beta_{\rm M} > 0$) that renders LLs steeper at lower metallicity at all wavelengths. Importantly, $\beta_{\rm M} \ne 0$ implies that the intercept-metallicity dependence, $\alpha_{\rm M}$, depends on pivot period; an issue not previously considered. Comparison with $\alpha_{\rm M}$ measurements in individual passbands reported in the literature yields acceptable agreement on the order of agreement found among different observational studies. The wavelength dependence and magnitude of the disagreement suggests a possible origin in reddening-related systematics. Conversely, we report excellent agreement between our $\alpha_{\rm M} = -0.20 \pm 0.03$ mag dex$^{-1}$ and the value determined by the SH0ES distance ladder in the reddening-free H-band Wesenheit magnitude ($-0.217 \pm 0.046$), the currently tightest and conceptually simplest empirical constraint.