Hanneke C. Woudenberg, Amina Helmi

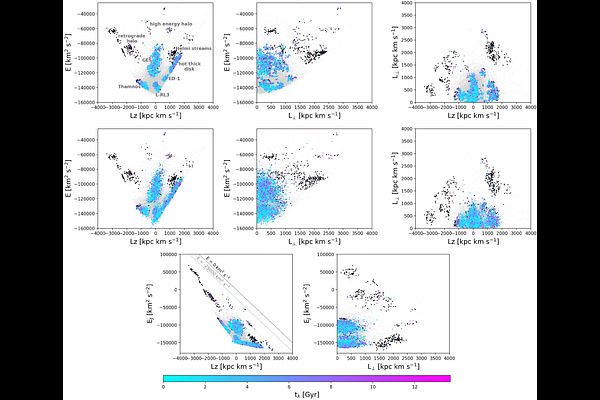
Many of the Milky Way's accreted substructures have been discovered and studied in the space of energy $E$, and angular momentum components $L_z$ and $L_{\bot}$. In a static axisymmetric system, these quantities are (reasonable approximations of) the integrals of motion of an orbit. However, in a galaxy like the Milky Way with a triaxial, rotating bar, none of these quantities are conserved, and the only known integral is the Jacobi energy $E_J$. This may result in chaotic orbits, especially for inner halo stars. Here, we investigate the bar's effect on the dynamics of nearby halo stars, and more specifically its impact on their distribution in $(E, L_z, L_{\bot})$ space. To this end, we have integrated and characterised the orbits of halo stars located within 1 kpc from the Sun. We computed their orbital frequencies and quantified the degree of chaoticity and associated timescales, using the Lyapunov exponent and the frequency diffusion rate. We find that the bar introduces a large degree of chaoticity on the stars in our sample: more than half are found to be on chaotic orbits, and this fraction is highest for stars on very bound and/or radial orbits. Such stars wander in $(E, L_z, L_{\bot})$ space on timescales shorter than a Hubble time. This introduces some overlap and hence contamination amongst previously identified accreted substructures with these orbital characteristics, although our assessment is that this is relatively limited. The bar also induces a number of resonances in the stellar halo, which are of larger importance for lower inclination, prograde orbits. Because the effect of the Galactic bar on the local halo is important for stars on very bound and/or radial orbits, clustering analyses in these regions should be conducted with care. Replacing the energy by $E_J$ in such analyses could be an improvement.