Schmutz, V.; Haydaroglu, A.; Wang, S.; Feng, Y.; Carandini, M.; Harris, K. D.

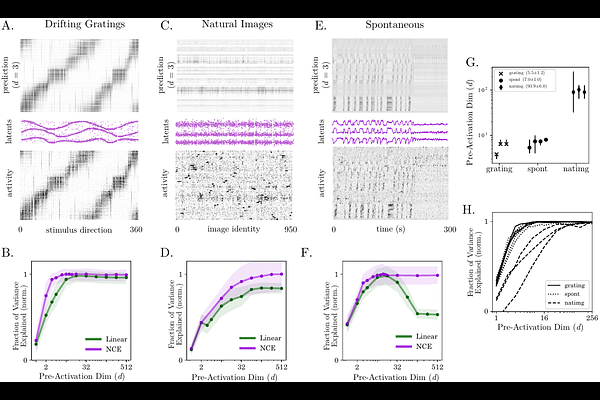
Computation in recurrent networks of neurons has been hypothesized to occur at the level of low-dimensional latent dynamics, both in artificial systems and in the brain. This hypothesis seems at odds with evidence from large-scale neuronal recordings in mice showing that neuronal population activity is high-dimensional. To demonstrate that low-dimensional latent dynamics and high-dimensional activity can be two sides of the same coin, we present an analytically solvable recurrent neural network (RNN) model whose dynamics can be exactly reduced to a low-dimensional dynamical system, but generates an activity manifold that has a high linear embedding dimension. This raises the question: Do low-dimensional latents explain the high-dimensional activity observed in mouse visual cortex? Spectral theory tells us that the covariance eigenspectrum alone does not allow us to recover the dimensionality of the latents, which can be low or high, when neurons are nonlinear. To address this indeterminacy, we develop Neural Cross-Encoder (NCE), an interpretable, nonlinear latent variable modeling method for neuronal recordings, and find that high-dimensional neuronal responses to drifting gratings and spontaneous activity in visual cortex can be reduced to low-dimensional latents, while the responses to natural images cannot. We conclude that the high-dimensional activity measured in certain conditions, such as in the absence of a stimulus, is explained by low-dimensional latents that are nonlinearly processed by individual neurons.