Saisandri Saini, Akhilesh Nautiyal

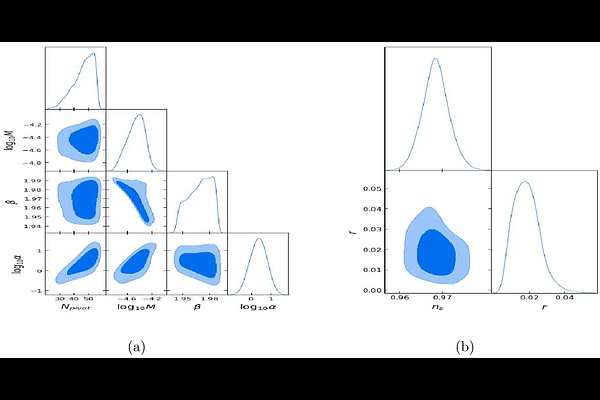
In this work we consider a generalization of Starobinsky inflation obtained by combining power law ($R^\beta$), and $\alpha$-Starobinsky inflation ($E$-model). The Einstein frame potential for this model is that of power law Starobinsky inflation modified by a parameter $\alpha$ in the exponential. After computing power spectra for scalar and tensor perturbations numerically, we perform MCMC analysis to put constraints on the potential parameter $\alpha$, $\beta$ and $M$, and the number of e-foldings $N_{pivot}$ during inflation, using Planck-2018, BICEP/Keck (BK18) and other LSS observations. We find $\log_{10}\alpha= 0.37^{+0.82}_{-0.85}$, $\beta = 1.969^{+0.020}_{-0.023}$, $M=\left(3.54^{+2.62}_{-1.73}\right)\times 10^{-5}$ and $N_{pivot} = 47\pm{10}$. We compute the Bayesian evidences for our proposed model, power law Starobinsky inflation, $\alpha$-Starobinsky inflation and Starobinsky inflation. Considering the Starobinsky model as the base model, we calculate the Bayes factor and find that our proposed model is preferred by the CMB and LSS observations.