MIRAGE: Quantum Circuit Decomposition and Routing Collaborative Design using Mirror Gates
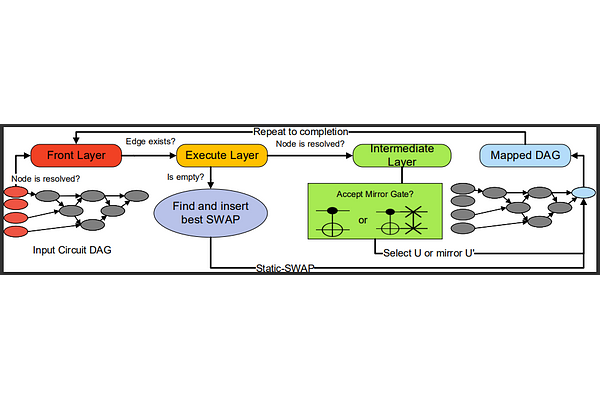
MIRAGE: Quantum Circuit Decomposition and Routing Collaborative Design using Mirror Gates
Evan McKinney, Michael Hatridge, Alex K. Jones
AbstractBuilding efficient large-scale quantum computers is a significant challenge due to limited qubit connectivities and noisy hardware operations. Transpilation is critical to ensure that quantum gates are on physically linked qubits, while minimizing $\texttt{SWAP}$ gates and simultaneously finding efficient decomposition into native $\textit{basis gates}$. The goal of this multifaceted optimization step is typically to minimize circuit depth and to achieve the best possible execution fidelity. In this work, we propose $\textit{MIRAGE}$, a collaborative design and transpilation approach to minimize $\texttt{SWAP}$ gates while improving decomposition using $\textit{mirror gates}$. Mirror gates utilize the same underlying physical interactions, but when their outputs are reversed, they realize a different or $\textit{mirrored}$ quantum operation. Given the recent attention to $\sqrt{\texttt{iSWAP}}$ as a powerful basis gate with decomposition advantages over $\texttt{CNOT}$, we show how systems that implement the $\texttt{iSWAP}$ family of gates can benefit from mirror gates. Further, $\textit{MIRAGE}$ uses mirror gates to reduce routing pressure and reduce true circuit depth instead of just minimizing $\texttt{SWAP}$s. We explore the benefits of decomposition for $\sqrt{\texttt{iSWAP}}$ and $\sqrt[4]{\texttt{iSWAP}}$ using mirror gates, including both expanding Haar coverage and conducting a detailed fault rate analysis trading off circuit depth against approximate gate decomposition. We also describe a novel greedy approach accepting mirror substitution at different aggression levels within MIRAGE. Finally, for $\texttt{iSWAP}$ systems that use square-lattice topologies, $\textit{MIRAGE}$ provides an average of 29.6\% reduction in circuit depth by eliminating an average of 59.9\% $\texttt{SWAP}$ gates, which ultimately improves the practical applicability of our algorithm.