Qiao Yue, Zhaoyi Xu, Meirong Tang

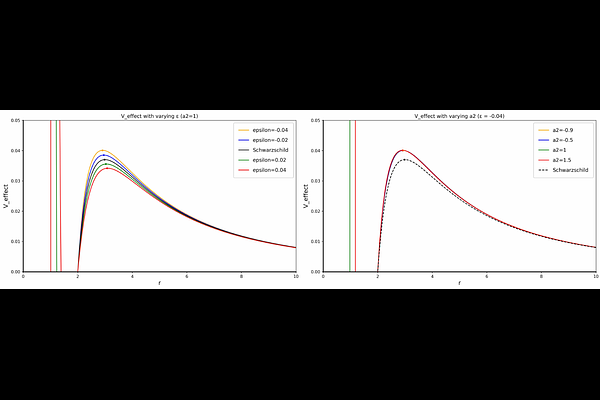
This research delves into the optical characteristics of stationary, spherically symmetric black holes. These black holes follow the Konoplya-Zhidenko deformation rule in arbitrary gravity theories. This research finds that the effects of \(a_2\) and \(b_2\) on photon orbital dynamics exhibit observational degeneracy, while \(\varepsilon\) significantly governs photon capture characteristics. As \(\varepsilon\) increases, the radius of the photon sphere \(r_{\text{ph}}\) and the critical impact parameter \(b_{\text{ph}}\), and the innermost stable circular orbit radius \(r_{\text{isco}}\) all increase. The event horizon \( r_{\text{h}} \) corresponds to that of the Schwarzschild black hole, while the impact parameter range for the lens and photon rings is reduced. Black hole shadow and photon ring analyses across three emission models show that increasing \(\varepsilon\) shifts the peak rightward while enlarging the photon ring radius. The closer \(\varepsilon\) is to zero, the more the results approach the Schwarzschild case, the more the results approach the Schwarzschild case. Additionally, by combining EHT observational data on the shadow diameters of M87 and Sgr A*, we imposed constraints on the correlation parameter \(\varepsilon\) in the theoretical model(at the confidence level anchored by \(d_{\text{sh}}^{(M87^*)}\), the parameter \(\varepsilon\) is confined to the interval \(-0.09 \lesssim \varepsilon \lesssim 0.19\). For \(d_{\text{sh}}^{(Sgr A^*)}\), the constraint on \(\varepsilon\) is delineated as \(-0.280 \lesssim \varepsilon \lesssim 0.047\)). The results show that within the observationally allowed range of \(\varepsilon\) (such as \([-0.04, 0.04]\)), the characteristics of the black hole exhibit specific regularities with changes in \(\varepsilon\).