N. V. Krishnendu, Aldo Perri, Sumanta Chakraborty, Alessandro Pesci

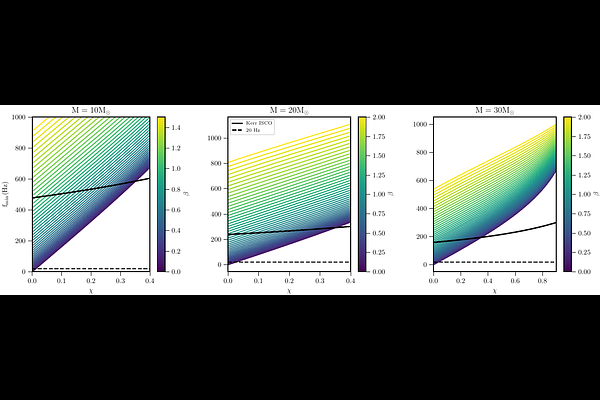
Existence of a minimal length in spacetime geometries avoids several singular situations involving quantum theory and gravity. In this work, we show that the existence of such a minimal length also affects the gravitational wave (GW) waveform of any inspiraling binary black hole (BH) system by introducing a minimum frequency, below which the BHs behave as perfectly reflecting compact objects, while above they are identical to classical BHs. This leads to a significant imprint on the tidal heating term, appearing in the GW waveform at 2.5 post Newtonian order. Based on these modifications to the inspiraling waveform, it turns out that the detection of highly spinning and highly absorbing, almost classical BH like compact objects, inspiraling around each other, would be in tension with the quantum properties of BH geometries. The same would also be true if the zero point length exceeds the Planck length by a significant amount, suggesting that the zero point length, if it exists, must be of the same order as the Planck length, or smaller, purely from GW observations.