Rajdeep Paul, Sneha Munshi, Alok Kumar Pan

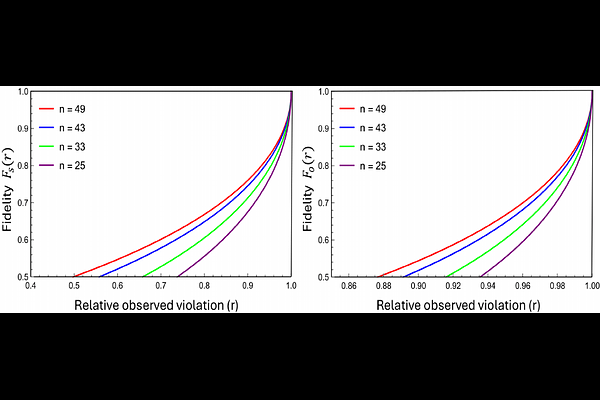
Self-testing is the strongest certification procedure that uniquely characterizes the physical system based on the observed statistics, without any knowledge of the inner workings of the devices. The optimal quantum violation of a Bell inequality enables such a device-independent (DI) self-testing of the source and the measurement devices. In this work, we demonstrate the DI self-testing based on the chained Bell inequality. We devise an elegant sum-of-squares (SOS) technique enabling dimension-independent optimization of the quantum violation. Our approach enables the derivation of the state along with the relationship between the local observables directly from the optimization condition. This improves the previous methods of self-testing by deriving the state from the self-testing relation instead of assuming that the state is restricted to a two-qubit system. One significant aspect is the robustness of such self-testing in real experimental situations involving noise and imperfection, leading to deviation from the optimal quantum violation. We provide an analytical technique for robust self-testing in the presence of noise. As an application of our scheme, we demonstrate the generation of two bit DI randomness and analyze the robustness of such randomness.